

Validité d'un modèle
Domaine de validité d'un modèle
Le domaine de validité d'un modèle dépend
de la théorie à laquelle il est lié
Le domaine de validité d'un modèle dépend
des choix de son concepteur
Un exemple d'évolution du domaine de validité dans
le domaine de la recherche : les cellules HeLa
Exemples de formulation du domaine de validité au cours
d'une activité de classe
Pour aller plus loin
Notes
Dans l’enseignement secondaire [...], les travaux pratiques qui sont mis en œuvre consacrent peu de place à un travail sur les modèles en jeu. [...]Par ailleurs, ces modèles sont peu discutés, leur domaine de validité généralement non-défini.
Eric SANCHEZ, Place et rôle des modèles dans l'enseignement des sciences de la Terre
La difficulté, c'est qu'étant donnée la diversité des modèles mis en jeu, il n'est déjà pas évident de définir la notion de domaine de validité. De plus, pour la plupart des modèles utilisés en classe, on ne dispose pas du domaine de validité défini par l'auteur du modèle ni des données permettant éventuellement de le redéfinir...
Comment aborder cette difficulté ?
Un modèle est dit valide si il est capable de reproduire correctement les données observées.
Source : Raphaël Duboz,
Construire,
calibrer, valider un modèle Travailler avec des données,
IRD ( Institut de Recherche pour le Développement)
Cette définition a l'avantage d'être simple. Mais que signifie le terme "correctement" ?
Les critères permettant d'estimer l'adéquation
d'un modèle à une série de données relèvent
des mathématiques. Le plus simple à utiliser en classe est le
coefficient
de corrélation. Très critiquable, le coefficient de corrélation
a au moins l'avantage de fournir aux élèves un outil de décision
simple à mettre en oeuvre. En situation de recherche, d'autres outils
plus performants sont utilisés (tests de Student, de Fisher, du ![]() ...)
...)
On peut considérer le domaine de validité comme l'ensemble des conditions permettant au modèle d'être valide
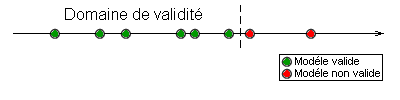
Fig. 1 : Représentation schématique du domaine de validité
La figure ci-contre correspond à un modèle très simple dépendant d'un seul paramètre numérique.
En réalité, les modèles - et notamment les modèles utilisés en recherche scientifique - dépendent d'une multitude de paramètres, numériques ou non. Dans l'absolu, il faudrait déterminer le domaine de validité pour chaque paramètre ; le domaine de validité du modèle correspondrait alors à l'ensemble des domaines de validité pour chaque paramètre.
Claudine Schmidt-Lainé et Alain Pavé [1] résument plus simplement cela en disant que le modèle ne doit pas pouvoir être mis en défaut par confrontation avec les données dans son domaine de validité (qu'ils appellent "domaine de confiance"). "En revanche, aucune assurance n'est donnée sur ses performances en dehors."
C'est très difficile à réaliser, souvent par manque de données. Voir des exemples dans le diaporama de Raphaël Duboz (op.cit.).
(voir la page théorie / modèle)
Les physiciens disposent d'un grand nombre de théories générales. Un modèle construit dans le cadre de l'une de ces théories sera souvent pas ou peu valide dans le cadre d'une autre théorie. La théorie participe à la détermination du domaine de validité du (des) modèle(s) au(x)quel(s) elle a donné naissance.
"Les propriétés que la relativité accorde au vide s'harmonisent mal avec ce qu'en déclare la physique quantique, et réciproquement, de telle sorte que les deux théories ne peuvent pas être vraies simultanément."
Marc Lachièze-Rey, Le statut du vide pose problème, La Recherche n°474, Avril 2013
Les naturalistes ne disposent pas de théories aussi larges, mais les théories de l'évolution [2] peuvent permettre une réflexion équivalente. Par exemple, le modèle proposé dans le module "Dérive génétique" de l'activité Biodiversité génétique est lié à la théorie neutraliste de Kimura [3] :
Finally, if my chief conclusion is correct, and if the neutral or nearly neutral
mutation is being produced in each generation at a much higher rate than has
been considered before, then we must recognize the great importance of random
genetic drift due to finite population number in forming the genetic structure
of biological populations. [4]
Kimura M., « Evolutionary rate at the molecular level », Nature, 217, 1968, p. 624 à 626.
|
L'activité Biodiversité génétique propose un module "Dérive génétique" basé sur la loi de Hardy-Weinberg. Celle-ci a été conçue dans le cadre de la théorie de l'hérédité (théorie mendélienne) qui cotoyait alors - sans interférer - la théorie de l'évolution darwinienne. La loi de Hardy-Weinberg (1908) stipule qu'on travaille sur une population "idéale" (voir ci-contre). Ces conditions définissent le domaine de validité du modèle utilisé. On perçoit rapidement à la lecture des critères de la population "idéale" qu'ils ne sont jamais respectés dans les conditions naturelles et donc qu'on est hors du domaine de validité du modèle. Mais c'est sur des bases mathématiques de ce type que Georges Teissier et Philippe L'Héritier développèrent la dynamique des populations (dans les années 30), notamment avec les drosophiles et les célèbres cages à population qui permettaient de s'approcher un peu plus de la "population idéale". "Pour la première fois dans l'histoire de la biologie une théorie mathématique a précédé et orienté la recherche expérimentale" Dobzhansky et Boesiger, 1968, p. 61 |
|
Puis Kimura a amélioré le modèle mathématique dans les années 60, avec un domaine de validité permettant de tester le modèle à l'aide de données (voir certains de ces tests sur le site de l'Université de Tours).
On voit avec cet exemple qu'un modèle n'a pas besoin d'être proche de la réalité pour stimuler la réflexion sur le phénomène étudié.
| Theodor Schwann est le père de la théorie cellulaire (1839) : les cellules ne sont pas des boites vides (Hooke, Van Leeuwenhoek...) mais elles constituent la structure élémentaire de tous les organismes vivants, elles en sont l'unité morphologique et physiologique. Parmi les modèles "naturels" (voir Typologie
des modèles), les cellules dites HeLa occupent une place
importante. Issues de cellules tumorales prélevées en
1951 sur une patiente (Henrietta Lacks, d'où leur nom), elles
possèdent une capacité exceptionnelle à se multiplier,
ce qui en facilita la culture.
Source : Asae Igarashi, Kyowa Hakko Kirin
Co., Ltd., Japan |
|
|
Mais dès 1973, on a remarqué sur des caryotypes de lignées
de cellules HeLa un nombre de chromosomes variant de 76 à 80
! Caryotype d'une cellule Hela |
 Licence Creative Commons |
Par chance, la méconnaissance de cette altération du génome n'a pas entravé la mise au point du vaccin contre la polio. Mais dans les utilisations futures des cellules HeLa, il conviendra de restreindre leur domaine de validité :
Utilisations possibles des cellules HeLa |
Utilisations impossibles des cellules HeLa |
|
|
Source : Voir note [6]
Dans toutes les activités de TP, il y a construction - le plus souvent implicite - d'un modèle : le savoir mémorisable (bilan de la séance) élaboré est un modèle didactique. Certaines séances donnent lieu à la construction plus explicite de modèles quantitatifs (par exemple équation d'un droite de régression) ou qualitatifs (par exemple sens de variation de la fonction testée, croissante ou décroissante).
Quand c'est possible, il serait souhaitable de faire prendre l'habitude aux élèves d'associer un domaine de validité, même partiel, au modèle élaboré. L'un des principaux avantages serait de permettre une prise de conscience par l'élève du caractère relatif du modèle élaboré et du savoir mémorisé.
| Activité | Modèle | Approche du domaine de validité |
| Déplacement des plaques lithosphériques (GPS) | linéaire | Intervalle de temps court (vitesse constante) |
| polynomial | Intervalle de temps long (vitesse variable) | |
| Nourrir l'humanité | compartimental | Agrosystème, bovins/maïs, France... |
| Organisation et fonctionnement du coeur | schéma | Mammifères (et oiseaux), fonction pulsatoire... |
| Biodiversité génétique | loi de Hardy-Weinberg | Voir ci-dessus |
| Pinsons des Galapagos | compartimental | Darwinisme, sélection naturelle... |
| Structure de l'ADN et nature du message codé | moléculaire | Température, résolution... |
| ... |
[1] Claudine Schmidt-Lainé et Alain Pavé, La modélisation au coeur de la démarche scientifique et à la confluence des disciplines , Les Cahiers du musée des Confluences, Lyon, 2008, p 21-34. Télécharger toute la revue ou seulement l'article. Retour
[2] Fixisme, catastrophisme de Cuvier, transformisme de Lamarck, sélection naturelle de Darwin, théorie synthétique de Dobzhansky et al., théorie neutraliste de Kimura... Retour
[3] Bien que le modèle proposé dans l'activité soit très simple - voire simpliste - par rapport à ceux de Motoo Kimura, spécialiste de modélisation mathématique. Retour
[4] "Si l’évolution neutre où presque neutre est produite à chaque génération à un degré plus élevé que ce que l’on pensait auparavant, alors nous devons reconnaître la grande importance de la dérive génique aléatoire due à une taille finie de population dans la formation de la structure génétique des populations biologiques." Retour
[5] J. Landry et al.,The Genomic and Transcriptomic Landscape of a HeLa Cell Line,G3, 2013. Cliquer sur "Full Text (PDF)". Si l'article s'affiche mal dans votre navigateur, faire un clic droit sur "Full Text (PDF)" puis "Enregistrer la cible sous...". Retour
[6] Oivier Micheau (Inserm Dijon) dans l'article de A. Debroise, Des cellules modèles bien loin de la réalité, La Recherche n°475, mai 2013. Retour