

Le travail précédent a permis d'évaluer la vitesse d'augmentation de la quantité de carbone émise au siècle dernier : c'est le coefficient directeur de la droite de régression (ou de tendance) associée au nuage de points.
En examinant ce nuage de points on s'aperçoit que cette vitesse de variation est loin d'être constante. On va essayer d'affiner l'analyse en comparant d'abord deux périodes : 1900-1949 et 1950-2000. Le fichier CO2math2.ods contient les informations nécessaires pour ces deux périodes.
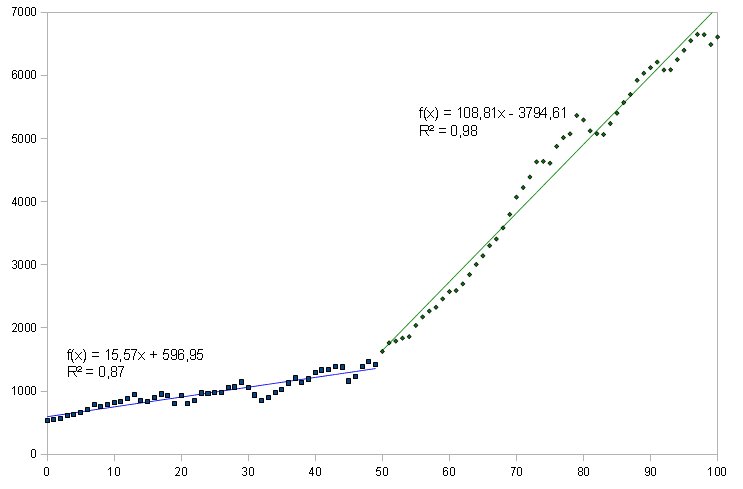
Question 1 : quelles sont les vitesses de variation pour chacune de ces deux périodes (dans le cas d'un modèle linéaire) ?
On remarque que la vitesse de variation sur la deuxième période est supérieure à celle sur la première ; on peut parler d'accélération des émissions entre ces deux périodes.
Cette division en intervalles dont la largeur tend vers 0 prépare l'introduction (en première) de la vitesse instantanée et donc de la notion de dérivée
La « courbe de tendance » est maintenant formée de deux segments : la fonction f qu'elle représente est une fonction affine par intervalles. Si on poursuit l'analyse dans ce sens on peut envisager d'augmenter (dans une certaine mesure) le nombre d'intervalles en diminuant leur amplitude.
Le tableur permet de tester des courbes de tendance qui ne seraient plus affines (par intervalles). Diverses possibilités existent et on va ici utiliser une courbe de tendance « exponentielle ».
Question 2 : en utilisant le fichier CO2math2.ods afficher la courbe de tendance exponentielle, la fonction f qu'elle représente et le coefficient de détermination ; comparer ce coefficient de détermination avec ceux précédemment obtenus.
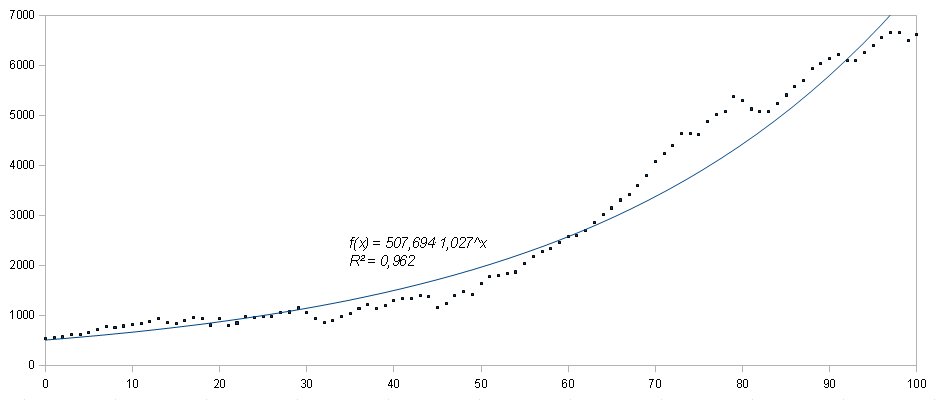
Question 3 : pour le modèle exponentiel peut on dire que la variation annuelle moyenne des émissions est constante ?
On utilise à nouveau ici le modèle comme outil de prévision (par extrapolation) ; en comparant avec le modèle linéaire de la première séquence on peut discuter de la validité des choix et de l'implication de ces choix dans le résultat des prévisions.
Question 4 : en utilisant le modèle exponentiel peut on prévoir les émissions futures (par exemple en 2020 et en 2050) ? Comparer avec les valeurs trouvées avec le modèle linéaire.
Dans le modèle linéaire on s'appuyait sur la notion de fonction affine (programme de seconde) ; en première on peut réinterpréter la vitesse moyenne constante en terme de suite arithmétique. Ceci permettra dans le modèle exponentiel de partir des suites géométriques (programme de première) pour interpréter le pourcentage avant d'en donner en terminale la formulation exponentielle.
Question 5 (complément) : à l'aide du tableur mettre en évidence le fait que sur le modèle exponentiel le pourcentage d'augmentation des émissions entre deux années consécutives est constant ; expliquer le lien entre cette propriété et l'expression algébrique de .